1: 2020/10/28(水) 07:27:38.310 ID:HaSZuXQq0
ただし0^0は定義されていないものとする
2: 2020/10/28(水) 07:27:59.575 ID:s6HX98tw0
1
4: 2020/10/28(水) 07:29:22.811 ID:HaSZuXQq0
>>2
やっぱそうなのか
やっぱそうなのか
3: 2020/10/28(水) 07:28:52.959 ID:doXnu/DHa
この場合0^0が定義されてる必要まったくないよな
5: 2020/10/28(水) 07:29:47.122 ID:HaSZuXQq0
>>3
そうなの?
0^0が定義されてたらそれがそのまま答えになるんじゃないの?
そうなの?
0^0が定義されてたらそれがそのまま答えになるんじゃないの?
6: 2020/10/28(水) 07:29:52.247 ID:JFouxv3y0
図描いてみろよ
7: 2020/10/28(水) 07:30:01.368 ID:doXnu/DHa
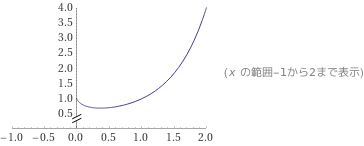
lim(x,y)→(0,0) x^y
これは不定だわ
z=x^yのグラフ見ればわかる
これは不定だわ
z=x^yのグラフ見ればわかる
10: 2020/10/28(水) 07:31:20.448 ID:iel+3SdR0
>>7
y=xに沿って0に近付けても?
y=xに沿って0に近付けても?
21: 2020/10/28(水) 07:40:04.794 ID:doXnu/DHa
>>10
y=x に沿った場合は
lim(x,y)→(0,0) x^y = lim x→+0 x^x = 1
やないか?(知らんけど)
y=0に沿ってx→+0とする場合はx=ε> 0とすると ε^0 = 1
x=0に沿ってy→+0とする場合はy=ε> 0とすると 0^ε = 0
8: 2020/10/28(水) 07:30:39.042 ID:HaSZuXQq0
いやよく考えたらそんなわけなかったわ
0^0=100とか定義されても
スレタイの極限が100になるわけないもんな
0^0=100とか定義されても
スレタイの極限が100になるわけないもんな
11: 2020/10/28(水) 07:33:02.826 ID:q+jtuabAd
0.1の10乗根が0.8くらい
0.01の100乗根が0.95くらい
0.01の100乗根が0.95くらい
13: 2020/10/28(水) 07:33:49.275 ID:HaSZuXQq0
>>11
やっぱ1っぽいな
やっぱ1っぽいな
38: 2020/10/28(水) 08:01:40.772 ID:P4afdUB60
>>11
これであってるぽいね
【質問】
累乗の計算で、乗数が0.1の場合計算を教えてください。
【ベストアンサー】
x^(0.1)=A とおくと
両辺10乗して
x=A^10
つまりAは10乗してxになる数です。
たとえば 2の0.1乗 とは 10乗して2になる数です。
このような計算では 0<x≠1 という前提条件が付いて負の数や複素数は考えないのが普通です。
具体的な計算方法は関数電卓を使うのが普通。
関数電卓がなければ常用対数表を使う。
2の0.1乗を計算したい場合、
A=2^(0.1)
対数表から log2≒0.3010 とわかるので
logA=0.1・log2=0.1・0.3010=0.03010
対数表を逆引きして
A≒1.07
12: 2020/10/28(水) 07:33:14.515 ID:y/z8tCTL0
lim x^x と lim x^(2x) とlim (2x)^x は別の値になる
一応全部x→0な
一応全部x→0な
14: 2020/10/28(水) 07:34:17.307 ID:xNJZbRIq0
定義されてたらその値だろ
20: 2020/10/28(水) 07:37:17.911 ID:HaSZuXQq0
>>14
俺も一瞬そう思ったけど違う
例えばf(x)が x=0のとき100、x≠0のときx^2 だったとして
lim x→0 f(x)の答えは100にはならずに0になる
俺も一瞬そう思ったけど違う
例えばf(x)が x=0のとき100、x≠0のときx^2 だったとして
lim x→0 f(x)の答えは100にはならずに0になる
15: 2020/10/28(水) 07:34:26.266 ID:HaSZuXQq0
え、これで不定なんてことがあり得るの?
16: 2020/10/28(水) 07:35:16.129 ID:xfKILplFp
x^x>>0
これで合ってるか?
19: 2020/10/28(水) 07:36:27.272 ID:xfKILplFp
>>16
ここから
x>>0っと
ここから
x>>0っと
17: 2020/10/28(水) 07:36:04.006 ID:xfKILplFp
というかまだ数1の途中までしかやってないからわからん
18: 2020/10/28(水) 07:36:24.674 ID:urgKDyRM0
こういうのはだいたいlogとる
22: 2020/10/28(水) 07:44:56.413 ID:1M+XVbc6d
24: 2020/10/28(水) 07:46:52.709 ID:HaSZuXQq0
>>22
これマジ?
極小値存在すんのかよ
今度は極小値がいくつなのか気になってきたわ
これマジ?
極小値存在すんのかよ
今度は極小値がいくつなのか気になってきたわ
26: 2020/10/28(水) 07:47:51.877 ID:doXnu/DHa
>>24
微分して0になるとこ探せ
俺はさすがにそろそろ飯食わなきゃ
微分して0になるとこ探せ
俺はさすがにそろそろ飯食わなきゃ
30: 2020/10/28(水) 07:49:23.121 ID:HaSZuXQq0
>>26
そっか微分して0になるとこが傾き0で極大値・極小値になるんだっけ
すっかり忘れてるわ
てかx^xって微分できんのか…?
そっか微分して0になるとこが傾き0で極大値・極小値になるんだっけ
すっかり忘れてるわ
てかx^xって微分できんのか…?
23: 2020/10/28(水) 07:45:21.436 ID:H59MTpdTp
(x^x) ←ひっくり返ってかわいい
25: 2020/10/28(水) 07:47:11.639 ID:JeF4YJBH0
(li° x°)o
27: 2020/10/28(水) 07:48:22.519 ID:cSdxLpHS0
不定だぞ
28: 2020/10/28(水) 07:48:36.893 ID:qRGpl74A0
35: 2020/10/28(水) 07:54:32.595 ID:qRGpl74A0
無言だったからアレですけど>>28が全てです
29: 2020/10/28(水) 07:49:02.069 ID:ZMmwd3Zz0
^3^
31: 2020/10/28(水) 07:49:51.055 ID:+LAULbXTd
x=1/eで極小
32: 2020/10/28(水) 07:50:57.896 ID:HaSZuXQq0
>>31
なんかそれっぽい
(求め方分からんけど)
なんかそれっぽい
(求め方分からんけど)
33: 2020/10/28(水) 07:53:11.896 ID:+LAULbXTd
こういうのは対数とって微分すればいい
34: 2020/10/28(水) 07:53:38.697 ID:1M+XVbc6d
x^x
=exp(log(x^x))
=exp(x log(x))
微分して
(log(x) + 1) exp(x log(x))
だから極小はlog(x)=-1のとき
つまりx=1/eだね
=exp(log(x^x))
=exp(x log(x))
微分して
(log(x) + 1) exp(x log(x))
だから極小はlog(x)=-1のとき
つまりx=1/eだね
36: 2020/10/28(水) 07:56:31.500 ID:HaSZuXQq0
>>34
理解した
天才やん
理解した
天才やん
37: 2020/10/28(水) 07:59:44.498 ID:HaSZuXQq0
x=exp(logx)ってのも忘れてたわ



コメント